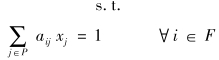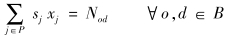-
0 引言
-
由于航空市场差异、机组人员(简称“组员”)分布不均等因素,航空公司经常出现各基地之间组员和航班任务数量不匹配的现象。为了保证航班任务全部被执行,组员多的基地必须支援组员少的基地(简称“跨基地派遣”)。因此,在任务环生成阶段,需要生成适量可满足机组人员跨基地支援的任务半环。目前,学术界对此类结合复杂业务场景的机组任务环问题的研究关注较少,主要考虑单基地或多基地的机组任务环优化问题[1-5]、机组任务环问题与机组人员派遣问题的一体化优化问题[6-8]、飞机路径问题或机型指派问题与机组任务环问题的一体化优化问题[9-10]以及机组任务环优化的鲁棒性[11-12]等业务场景。对此,杭州派迩信息技术有限公司(简称“派迩”)作为国内一家面向民航业智能化转型的公司,组建研究团队对国内航司面临的诸多业务、技术难题进行攻关,提出适用于国情的本土化解决方案。本文着重介绍考虑基地人员分布不均衡条件下的机组任务半环(简称“半环”)问题的解决方案。
-
首先,采用时空网络和集合划分模型对问题进行刻画。其次,采用列生成求解框架求解原0-1整数规划问题,将原问题分解为限制主问题(Restricted Master Problem)和最短时空路径子问题(The Time-Space Shortest Path Subproblem)。然后,详细讨论半环约束和其他约束的子问题目标函数项的本质区别,阐明半环约束的子问题目标函数项对列生成框架求解效率和质量的影响,提出可以保证消除该影响的分治策略,设计分支定价算法求解。最后,以某航空的实际数据进行验算。
-
1 问题描述
-
传统的机组任务环优化问题是根据《大型飞机公共航空运输承运人运行合格审定规则》第121条P章规定的和航空公司特有的机组排班规则,确定机组从各基地机场始发至回到同一基地机场过程中所执行的航段序列(如图1所示,基地为PEK)。但根据传统的任务环生成算法生成的完整任务环很难适用于派遣。因为在实际生产条件下,航空公司各基地的组员大都分布不均衡,组员除了飞行任务之外,还有各类培训、休假等任务,这些任务会在派遣优化之前预先分配,客观上会在短时间内加剧小基地机组资源的短缺。综合这些因素,在派遣阶段,如果已建好的任务环与属地资源不匹配,而派遣阶段又无法对任务环进行重构,再加上各种搭配规则问题的影响,那么必然导致部分飞行任务无法被覆盖。
-
图1 传统任务环示意图
-
为了解决上述问题,国内航司只能通过改变业务流程的方法来适配已有产品。目前业界普遍的做法是“派驻”,即在规定时间内,通过改变组员基地的方式,临时将组员从一个基地调动到另外一个基地支援一段时期(如:两个星期),组员以新的临时基地为中心,执飞隶属于这个基地的任务环。这种做法会造成一系列问题:
-
1)由于航班变化较大、机组人员其它任务(如培训,备份,带飞等)较多等因素的影响,计划人员很难精确制定派驻人员的数量和时间窗口。
-
2)机组人员驻外时间过长,会影响组员的满意度,影响机队稳定性。
-
3)组员在驻外期间的利用率一般较低,同时驻外期间的住宿、津贴等成本会大幅增加。
-
综上所述,基于“全环”的自动派遣方案和基于“派驻”的手工派遣方案均无法满足航司实际需求。若基于“半环”进行派遣,则可以有效缓解上述问题。不同于传统的任务环,半环的基本理念是,任务环的起始和终止站点可以不相同。以图2为例,资源充足的PEK基地,组员可以支援SHA基地的任务环。首先,任务环优化搭建出PEK-SHA,SHA-PEK的半环,以及SHA-SHA的任务环。然后派遣优化将半环与外基地任务环搭配组合,以达到最佳利用率。PEK基地的组员按顺序执飞(或乘机)PEK-SHA的半环,到达SHA后执飞SHA本地任务环,此后再执飞SHA-PEK半环回到组员本基地。
-
图2 人员派遣方案示意图
-
在图2案例中,通过半环搭桥,灵活衔接外基地任务环的优点就被充分体现出来,该方案可以同时考虑组员任务的时间连续性与空间连续性,实现了更为灵活的派遣优化。因此,本文针对半环生成方案进行研究。
-
机组排班问题的一般通用规则(以飞行机组为例)如下:
-
(1)飞行时间限制:机组成员实际执行飞行任务的总时间满足表1中的条件。
-
(2)飞行执勤期限制:机组成员出乘报道至签出退乘的时间满足下表2中的条件。
-
(3)休息期:机组到达休息场所至执行下一次任务离开休息场所的时间称为“休息期”,该时间必须不小于最小休息期minRestTime,通常取10 h。
-
(4)过站时间: 机组连续执飞两个任务中间在机场的停留时间称为“过站时间”,该时间必须不小于最小过站时间minConnTime。
-
(5)任务环长度:任务环的总长度不能超过最大任务环长度maxPairingLength,通常取4日历天。
-
(6)搭机置位数量:为执行飞行任务,允许机组人员以旅客的身份搭机前往执飞目的地。排班周期内,搭机总量不超过N1个。
-
(7)各基地间机组相互支援的任务半环数量:排班周期内,必须保证生成规定数量Nod的任务半环,以满足各基地间的机组相互支援。
-
2 网络创建
-
2.1 航段连接网络
-
考虑同城机场的航段连接网络需要将地面交通段(Ground activity)、搭机置位段(Deadhead)等节点和对应的弧加入到一般航段连接网络中。定义节点i(Segment),有开始时刻is、结束时刻ie、开始机场io、结束机场id四个属性; 构建航段连接网络
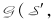
 =F ∪FD∪G,F为航段集合,FD为置位航班集合,G为地面交通段集合,O为虚起点,D为虚终点,弧集合
=F ∪FD∪G,F为航段集合,FD为置位航班集合,G为地面交通段集合,O为虚起点,D为虚终点,弧集合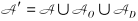 。对于任意两节点i,j∈
。对于任意两节点i,j∈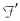 ,(i,j)∈
,(i,j)∈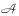 的连接条件满足id=jo且js-ie=[tc,tr]。 tc为最小连接时间,tr为最小休息时间。对于任意i∈
的连接条件满足id=jo且js-ie=[tc,tr]。 tc为最小连接时间,tr为最小休息时间。对于任意i∈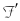 ,建立虚起点弧(O,i)∈
,建立虚起点弧(O,i)∈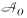 ,虚终点弧(i,D)∈
,虚终点弧(i,D)∈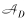 。考虑同城机场的航段连接网络图如图3所示,其中n为节点编号。图3(b)详细阐述航段连接网络中部分节点的详细连接情况。其中,连接(1)考虑同城基地间的地面置位(节点2n+1); 连接(2)考虑同城机场的地面置位(节点2n+2); 连接(3)考虑搭机置位(节点n+1)。
。考虑同城机场的航段连接网络图如图3所示,其中n为节点编号。图3(b)详细阐述航段连接网络中部分节点的详细连接情况。其中,连接(1)考虑同城基地间的地面置位(节点2n+1); 连接(2)考虑同城机场的地面置位(节点2n+2); 连接(3)考虑搭机置位(节点n+1)。 -
图3 航段连接
-
2.2 任务连接网络
-
基于航段连接网络,生成任务连接网络。首先,应用深度优先搜索算法(Depth-First Search,简称DFS)生成单日任务,利用飞行时间、飞行执勤期等规则进行剪枝加速。然后建立任务连接网络。定义任务连接网络
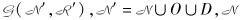 为任务集合,弧集合
为任务集合,弧集合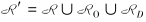 ,包括任务节点i∈
,包括任务节点i∈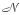 ,虚拟起点O、虚拟终点D、任务连接弧
,虚拟起点O、虚拟终点D、任务连接弧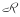 、虚拟起点弧
、虚拟起点弧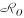 和虚拟终点弧
和虚拟终点弧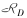 。与航段连接网络种组成弧的条件不同,对于任意两个任务i,j∈
。与航段连接网络种组成弧的条件不同,对于任意两个任务i,j∈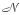 ,弧(i,j)∈
,弧(i,j)∈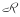 的连接条件为:id =jo且js-ie=[tr,tp ],tr为最小休息时间,tp为任务环最长时间。定义集合
的连接条件为:id =jo且js-ie=[tr,tp ],tr为最小休息时间,tp为任务环最长时间。定义集合 表示基地集合,对于任意任务i∈
表示基地集合,对于任意任务i∈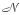 ,如果io∈
,如果io∈ ,建立虚起点弧(O,i)∈
,建立虚起点弧(O,i)∈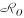 ,如果id∈
,如果id∈ ,则建立虚终点弧(i,D)∈
,则建立虚终点弧(i,D)∈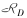 。
。 -
考虑同城机场的任务连接网络(Duty Connection Network)允许单一任务中置位(图4(a))和任务间置位(图4(b))。
-
图4 任务连接网络
-
3 数学建模
-
基于任务时空网络创建机组任务环优化问题模型,并将其分解为限制主问题模型和子问题模型。
-
3.1 原问题模型
-
机组任务环优化问题需要在大规模的任务环集合中选取满足业务规则且覆盖所有航段的最优任务环子集合,因此该问题可抽象为集合划分问题,具体模型为:
-
式中: xj为决策变量,表示任务环j; P为所有可行任务环集合; B为基地集合; cj表示任务环的成本; F表示航段集合; bj表示任务环j中包含的搭机置位数量; sj表示任务环j是否为起点为o终点为d的半环,若是取1,否则取0; N1代表搭机置位总量限制; Nod代表同城机场任务环总量限制。式(1)表示成本最小的总目标,具体细节见4.3章节; 式(2)表示所有航段必须被覆盖1次; 式(3)表示总搭机置位次数不能超过搭机置位总量限制; 式(4)表示各基地间相互支援的半环数量必须按规定生成限制; 式(5)表示决策变量为0-1决策变量。
-
3.2 限制主问题模型
-
原问题模型为NP-Hard问题,且列举所有可行任务环几乎不可能。因此,本文采用列生成策略进行求解,将原问题决策变量由0-1型松弛为连续型即可得到限制主问题模型。
-
3.3 最短路径子问题模型
-
3.3.1 带有资源约束的最短时空路径子问题
-
子问题设计的合理性是列生成框架求解质量的保证,由于机组任务环优化的原问题是基于时空网络的集合划分问题,该类问题的列生成子问题通常是带有资源约束的最短路径问题,需要求出满足资源约束且使检验数为负的最短时空路径。因此,本文子问题的目标函数可表示为:
-
式中,下标j表示列索引; uj表示任务环的任务数量成本; vj表示搭机置位成本; wj表示机组跨基地支援成本; πi表示航段覆盖约束对应的单纯形乘子; aij表示航段覆盖约束对应的系数; ηb表示搭机置位总量约束对应的单纯形乘子; bj表示搭机置位总量约束对应的系数; θod表示半环生成总量约束对应的单纯形乘子; dj表示半环生成总量约束对应的系数。式(6)表示最短路径问题的总目标,等价于原问题的线性松弛问题时列j的检验数。
-
3.3.2 子问题项的区别
-
机组任务环优化子问题的解对应一条“最短”任务环,通常由路径搜索算法沿任务时空网络搜索得出。任务环由任务序列组成,而任务由航段序列组成,若子问题目标中的各项能拆解至任务时空网络的各点或弧上,则有助于路径搜索算法的剪枝,加速求解; 否则,求解效率大大降低。因此,子问题的各项也可以根据任务环、任务、航段三个粒度进行拆解。由式(6)可知,子问题的总目标由任务环的任务数量成本项、航段覆盖检验数项、搭机置位检验数项和半环检验数项4项组成。拆解结果如表3所示。
-
4 基于分治策略的分支定价算法
-
4.1 子问题求解
-
子问题的求解难点在于两处:(1)带有任务环长度限制的资源约束;(2)半环生成总量约束的子问题目标函数项无法拆解到航段或者任务粒度。针对难点(1)通常采用多标签最短路算法求解,缺点在于多标签占优更新机制难以设计且极大地影响求解效率; 针对难点(2)通常采取近似策略或枚举策略解决,缺点分别在于损失求解精度和影响求解效率。因此,本文基于分治策略,设计并行搜索算法,解决上述难点。
-
分治策略思想为:
-
(1)将子问题资源约束分解,使其转变为无资源约束的最短路径问题,采用高效的最短路算法求解;
-
(2)将半环生成总量约束的子问题目标函数项分解,使需要支援的基地单独解子问题,即1个子问题只解决1对基地的半环生成问题。此时,子问题目标函数为,当目标函数值<时加入列池。
-
假设有m个基地、n个需要生成半环的基地对,并行搜索算法步骤为:
-
步骤1:复制m +n个任务时空网络;
-
步骤2:在m +n个任务时空网络上,并行求解m个基地的完整任务环问题和n个基地对的半环问题;
-
步骤3:将所得到的检验数为负的路径加入列池。
-
4.2 限制主问题求解
-
限制主问题为线性规划问题,调用商业求解器CPLEX求解。
-
4.3 原问题求解
-
本文采用分支定价算法求解原问题。该算法思想为:运用分支定界算法解决整数规划问题,针对根节点和各级分支节点的线性松弛问题,调用列生成算法求解如图5所示。
-
列生成算法步骤为:
-
步骤1:求解现有列池的限制主问题,记录各约束的单纯形乘子;
-
步骤2:根据单纯形乘子信息,调用子问题算法求解;
-
步骤3:若步骤2得到新的最短路径,则返回步骤1,否则,停止算法。
-
图5 列生成算法流程图
-
4.4 启发式分支策略
-
通过列生成算法求解得到线性松弛问题为原问题解的下界,为了获得整数解,本文采用CPLEX求解根节点的原混合整数规划问题。该问题属于NP难问题,当问题规模增大时,直接采用商业软件难以在可接受的时间范围内求解。为了加快求解速度,本文设计逐步迭代,近似逼近的启发式分支策略。
-
首先记迭代次数为i=0,判断根节点的线性松弛解是否为整数解,若不为整数解,进行分支,将原始解值大于或等于阈值 ε=ε0-i *δ的变量固定为1,δ为固定步长,ε0为初始阈值,同时将“冲突”列的对应变量固定为0。若两个列所覆盖的航段有交集,则二者冲突,不可能同时出现在最优解中。然后再次求解固定后的线性松弛问题,i =i +1,如此不断迭代,直至迭代次数i达到最大迭代次数或阈值小于设定值εlb时,重新求解带固定变量的混合整数线性规划模型。
-
5 案例分析
-
以某航空公司脱敏后的实际运营数据为例进行验证和分析。算法求解硬件环境为AMD Ryzen 5 3500U 2.10 GHz,8 GB的个人计算机。限制主问题利用商业求解器CPLEX12.10求解,航段时空网络的创建、任务生成的DFS算法、任务时空网络的创建、列生成算法及分支定价算法均利用C++语言编程实现。本实验测试的航班数据包括7 484个航段,计划周期为35天,由于篇幅原因,仅列出部分数据,如表4所示。采用的规则参数设置如表5所示:
-
根据各项输入,采用本文设计的优化方法求解考虑基地人员分布不均衡条件下的机组任务半环问题,得到的结果与实际人工手排结果的指标对比见表6,求解算法的统计信息见表7。
-
由表6和表7可知,本文提出的优化方法可以在较短时间内获得大规模考虑基地人员分布不均衡条件下的机组任务半环问题的最优解。在计算过程中,带有资源约束的最短路子问题的求解效率较高,且最终的列池规模较小,说明本文基于分治策略设计的子问题算法能够搜索得到质量良好的列,加快收敛速度。
-
6 结论
-
本文针对考虑基地人员分布不均衡条件下的机组任务半环问题进行研究,分析了传统的基于任务环的两阶段优化算法难以适用于该问题的原因,首次提出了任务半环的概念和生成方法,以满足跨基地支援派遣的需求。详细论述了半环生成总量约束的子问题目标函数项对传统的集合划分模型加列生成的求解框架的影响。提出了可分治并行的子问题求解策略,并用实际数据验证了该策略的效果。丰富了机组任务环优化问题的研究,为基地人员分布不均衡的机组排班问题的任务环优化阶段提供了有效的解决方案。
-
参考文献
-
[1] 李耀华,秦如如.基于混合遗传算法的航班串优化模型研究[J].中国民航大学学报,2010,28(6):31-34.
-
[2] 沈中林,李廷朵.遗传算法在航班覆盖问题中的应用研究[J].中国民航大学学报,2008,26(6):5-9.
-
[3] 石丽娜,唐小卫.基于二次遗传算法的机组任务配对问题研究[J].计算机工程与设计,2008,29(5):1244-1247.
-
[4] 蓝伯雄,张米.机组排班的混合集合规划方法研究[J].运筹与管理,2014(2):175-182.
-
[5] 赵正佳.航空公司机组排班计划研究[J].运筹与管理,2011(6):106-113.
-
[6] GUO Y,MELLOULI T,SUHL L,et al.A partially integrated airline crew scheduling approach with time-dependent crew capacities and multiple home bases[J].European Journal of Operational Research,2006,171(3):1169-1181.
-
[7] CHEN C,LIU T,CHOU J.Integrated short-haul airline crew scheduling using multiobjective optimization genetic algorithms[J].IEEE Transactions on Systems,Man,and Cybernetics:Systems,2013,43(5):1077-1090.
-
[8] ZEIGHAMI V,SADDOUNE M,SOUMIS F.Alternating lagrangian decomposition for integrated airline crew scheduling problem[J].European Journal of Operational Research,2020,287(1):211-224.
-
[9] SOUAI N,TEGHEM J.Genetic algorithm based approach for the integrated airline crew-pairing and rostering problem[J].European Journal of Operational Research,2009,199(3):674-683.
-
[10] VALENTINA C,JUAN-JOSÉ S.Optimal solutions to a real-world integrated airline scheduling problem[J].Transportation Science,2017,51(1):250-268.
-
[11] 蓝伯雄,张米.考虑延误因素的机组排班模型研究[J].中国管理科学,2015(12):167-176.
-
[12] 牟德一,王志新,夏群.基于机组延误概率的鲁棒性机组配对问题[J].系统管理学报,2011,20(2):207-212.
-
摘要
国内很多航空公司多基地间存在机组人员和航班任务数量不匹配的情况,导致各基地生成的任务环在机组派遣阶段难以被很好地执行,因此需在任务环生成阶段生成适量的可满足机组人员跨基地支援的任务半环,而传统的生成完整任务环的方案难以适用于该情况。在该问题中,通过顺序方法找到全局最优解是不可能的,因为在配对问题中做出的决策减少了机组分配问题的决策域。对此,创新性地提出了任务半环生成方案,并且创建基于时空网络的集合划分模型,分析任务半环生成总量约束的子问题目标函数项对列生成求解框架的影响,提出可以有效消除该影响的分治策略,采用实际数据验证算法可行性和有效性。与传统的方法相比,可显著节省成本并更好地满足机组人员分配不平衡问题。
Abstract
The mismatch between the number of crew and flight duties is widely occurred in airlines with multiple bases, which results in bad assignment at crew rostering stage. This problem can be fixed by generating partial pairing across bases, which is not considered in the traditional crew pairing generation method. Finding a globally optimal solution via the sequential approach may be impossible because the decision domain of the crew assignment problem was reduced by decisions made in the pairing problem. This paper proposes a new study of a crew pairing problem with partial pairing. A set partitioning model with partial pairing constraint based on segment time-space network firstly developed. To eliminate the effect on objective in subproblem caused by the additional constraint, a divide and conquer strategy was put forward. Finally, an empirical study was presented to validate the efficiency of the proposed algorithm. Compared with the traditional method, the method in this paper can significantly save costs and better meet the problem of crew mismatch.